Entenda como funciona o algoritmo de Cluster K-Means

Em uma forma lúdica para explicar o conceito

Fala galera, entenda o funcionamento do algoritmo de agrupamento K-Means, que é uma das formas que existe para se trabalhar com aprendizagem de máquinas (machine learning) no paradigma de aprendizado não supervisionado. Isso é diferente do aprendizado supervisionado, onde você informa ao computador o que ele deve procurar e aprender, com exemplos contendo os rótulos previamente. No aprendizado não supervisionado a gente não sabe exatamente o que estamos tentando ensinar ao computador. Por causa disso precisamos recorrer à agrupadores lógicos de segmentação, com foco em encontrar similaridade entre os dados da amostra.

O resultado esperado é que seja encontrado um padrão e assumir que este padrão é o que estamos tentando ensinar ao computador, que por sua vez, vai reproduzir e encontrar esse padrão sempre quando for solicitado. Depois de descoberto o padrão, qualquer item novo que tenha uma similaridade com aquele segmento (agrupamento [cluster, em inglês]) pode ser inferido como “fazendo parte daquilo”.

A proposta deste post é mostrar, com um certo nível de detalhes, como segmentar a amostragem em grupos e descobrir padrões nos dados. No final do texto você conseguirá ver uma referência para a implementação em Linguagem R, mas nesta publicação teremos o foco no entendendo o algoritmo.

Agrupando os dados

Para exemplificar, pense em um dataset com algumas amostras dispostas nos eixo X e Y, como o gráfico abaixo. Seu objetivo é agrupar estes dados baseado em sua similaridades (ou aproximação). Consegue fazer isso?

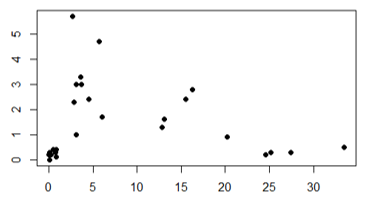
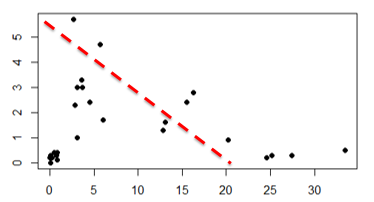
É possível bater o olho neste gráfico e ver a separação em alguns grupos. Mas cada um de nós que olhar o gráfico pode tentar criar um número diferente de grupos (clusters). Até mesmo quando a quantidade de cluster que pensarmos for igual, pode-se pensar em agrupamentos de formas diferentes. Por exemplo, alguns de nós podem ver a separação com apenas 2 clusters, e o gráfico poderia ser assim:

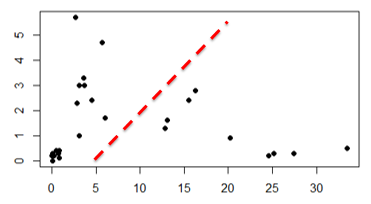
Ou assim…

Alguém também poderia pensar em separar os dados assim…

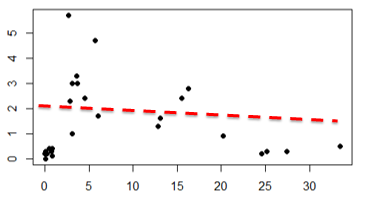
Qual é o certo? Todos estão certos! Isso pode acontecer de acordo com a interpretação de cada um dos observadores que encontraram apenas 2 grupos nestes dados.

Outras pessoas podem encontrar 3 grupos, e não apenas dois, podendo chegar a definições como esta:

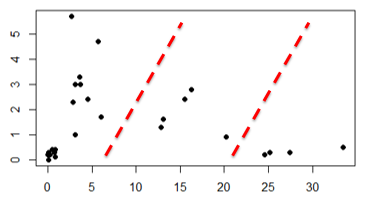
Ou esta

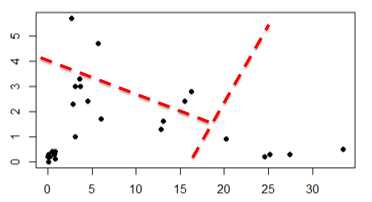
Ou então essa

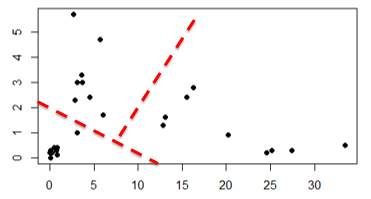
E aqui, qual dos gráficos é o certo? O certo é com 2 grupos ou com 3 grupos? Mais uma vez isso é difícil de responder, todos os 6 gráficos estão corretos de acordo com a visão de cada observador.

Entendendo como funciona o algoritmo de agrupamento K-Means

Para entender o funcionamento vamos separar os dados em 2 clusters e entender os passos que o algoritmo de agrupamento K-Means faz para convergir em um resultado. Neste caso o K será igual a 2, criando os 2 clusters que estamos buscando. O K, de K-Means, é a quantidade de centroides (pontos centrais dos grupos) que serão criados e ajudará a encontrará a similaridade dos dados.

Uma das formas de iniciar o processo é o algoritmo inserir o K pontos (centroides) aleatórios iniciais. Pode ser qualquer lugar do plano, para em seguida começar as iterações e encontrar os resultados.

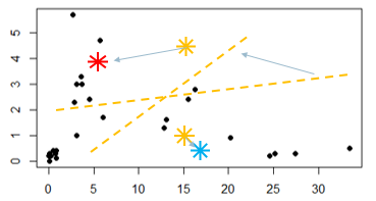
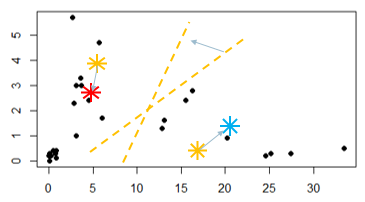
Veja dois pontos aleatórios criados no gráfico, e uma linha tracejada que é calculada aproximadamente na metade da distância dos pontos Vermelho e Azul. Com este segmento, os itens que estão plotados acima da linha tracejada fazem parte do grupo vermelho e os de baixo da linha fazem parte do grupo azul.

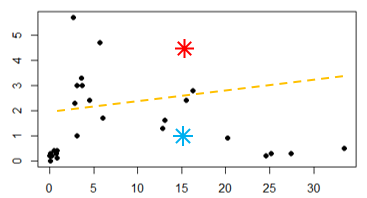
A primeira iteração do algoritmo é medir a distância de todos os pontos que estão atrelados ao centroide e então calcular sua média. O resultado gera uma nova coordenada de X e Y, e vai mudar a posição do centroide para o novo ponto que foi calculado, que é a distância média de todos os pontos que se ligaram à aquele centroide. Essa mudança de posição do centroide pode alterar os itens que fazem parte daquele grupo. Veja isso nas imagens abaixo:

O ponto vermelho e azul se moveram baseados na distância média dos elementos que estavam atrelados à aqueles centroides.

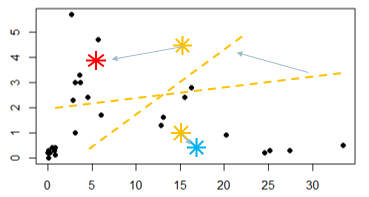
Após essa movimentação, a linha tracejada muda sua posição e inclinação.

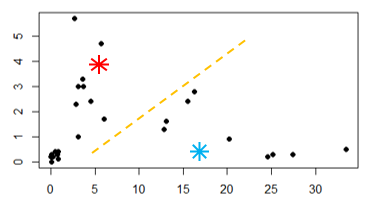
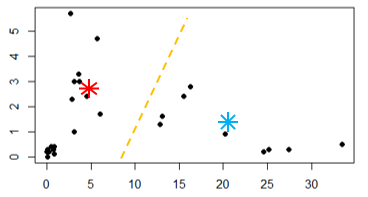
Reparem que alguns pontos pretos que faziam parte de um grupo na iteração anterior, como resultado, mudaram-se para o outro grupo.

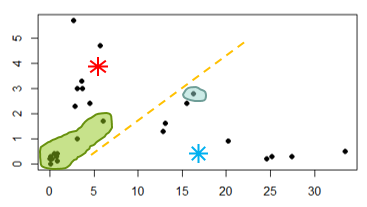
E quando ele vai convergir?

Com essa mudança de grupos, os pontos que estão marcados em verde passaram do centroide azul para o vermelho, e o que está marcado em azul passou do centroide vermelho para o azul. É possível reparar que a iteração de cálculo da média da distância dos pontos até o centroide ocorre em loop, até que nenhum ponto mude mais de centroide. Em outras palavras, isso acontece quando os centroides param de atualizar suas posições, porque já estão na posição central da distância entre os pontos. Chamamos isso de convergir!

Repare mais algumas possíveis iterações dos centroides e sua linha tracejada imaginária.

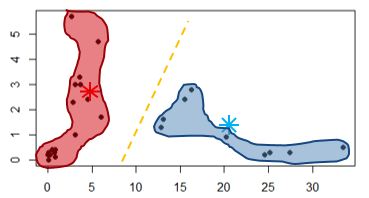
Veja que entre a penúltima iteração e esta não ouve mais mudança de pontos entre o gráfico e o centroide, portanto o algoritmo de agrupamento K-Means encerra sua execução chegando ao resultado esperado e criando dois grupos. Por exemplo, quando um novo item for incluído no gráfico, ele já terá um grupo que atende aquela região e o computador já saberá do que se trata o dado novo.

Escolhendo a quantidade de K (clusters) no algoritmo de agrupamento K-Means

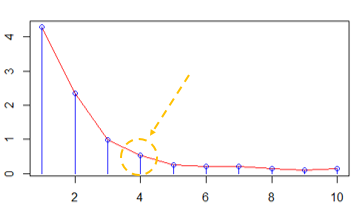
O Elbow Method é uma das formas usadas para descobrir a quantidade ideal de clusters naquele conjunto de dados. Ele tem esse nome por se parecer com o formato de um “braço” e nós sempre procurarmos o “cotovelo” pra definir que este é o número aceitável de K (grupos) a serem criados com base nos dados da amostra. Este método vai aumentando a quantidade de clusters a partir de 1 e analisando o resultado melhorado a cada incremento. Quando o benefício parar de ser relevante (um salto entre uma quantidade de cluster e a próxima quantidade) ele entra em um modelo platô, no qual a diferença da distância é quase insignificante. Ou seja, é neste momento que entende-se que o algoritmo é relevante com aquela quantidade de K e então ele deve ser usado pra segmentar os dados do gráfico.

Depois de executar o código do algoritmo do Elbow Method e olhando para os dados que estamos apresentando como exemplo, um bom número de K para ele é o número 4.

Rodando o algoritmo com 4 centroides, foi possível ver a transformação acontecendo e gerando esta segmentação:

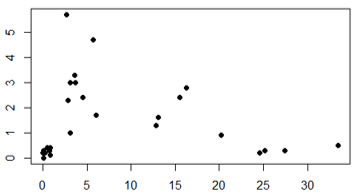
Conjunto inicial de dados

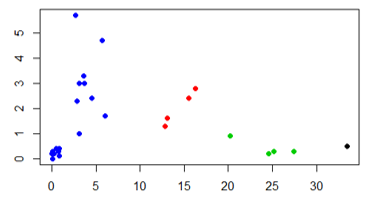
Após a execução do algoritmo e cada grupo representando uma cor

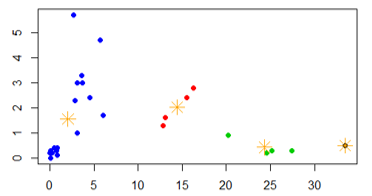
A posição dos centroides finais, para cada grupo

Para continuar os estudos…

A proposta desta publicação foi explicar de forma lúdica como o algoritmo de agrupamento K-Means funciona, mas você pode acompanhar uma implementação em R e depois ler sobre as possibilidades de implementar também com Azure Machine Learning.

Para ajudar a responder a questão de quantos grupos devem existir neste conjunto de dados, alguns métodos são bem aceitos no meio científico, leia mais sobre eles aqui: https://en.wikipedia.org/wiki/Determining_the_number_of_clusters_in_a_data_set.